Methods

Graph neural networks

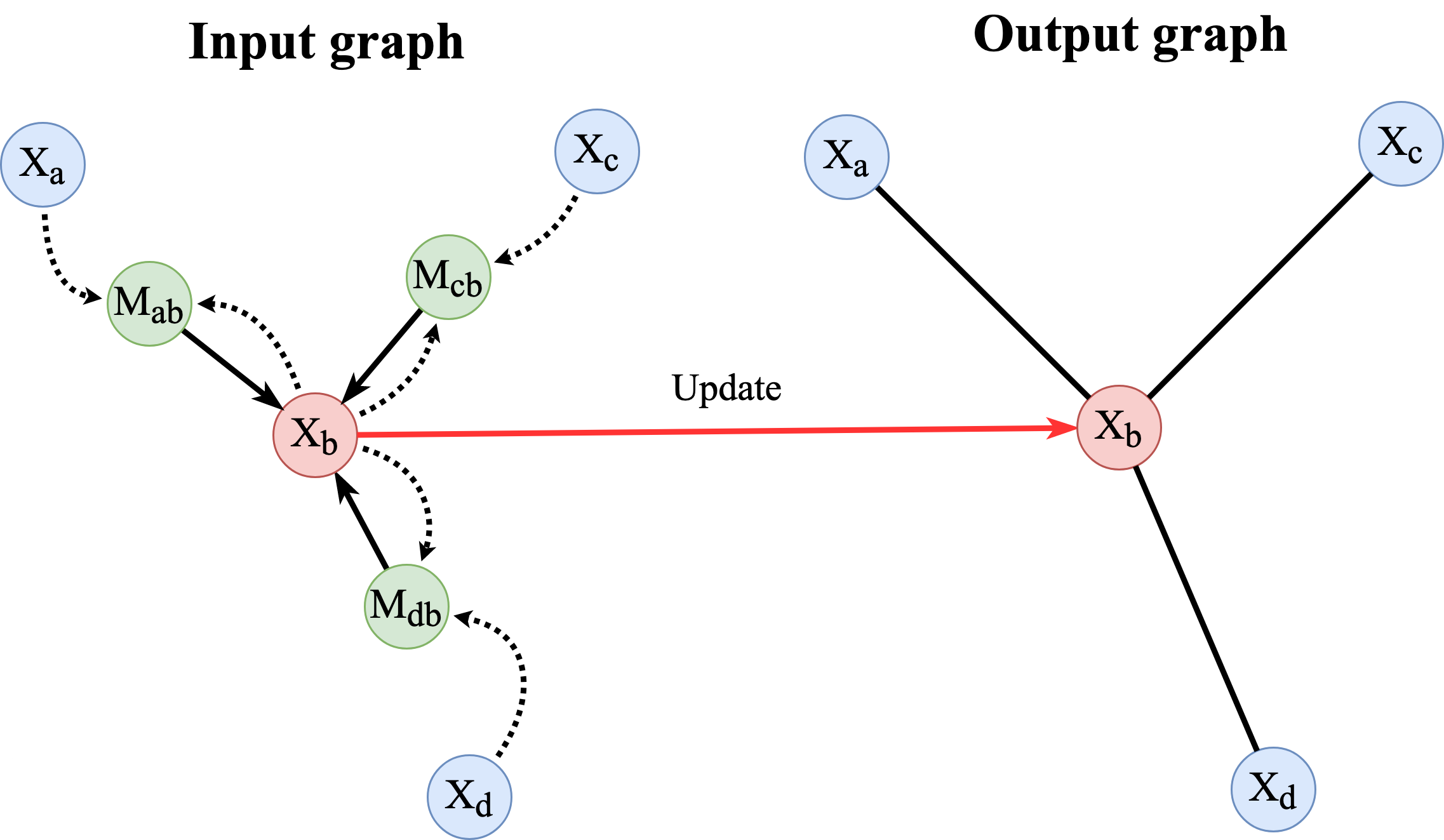
Graph Neural Networks (GNNs) (Battaglia et al. 2018Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-Gonzalez, A., Zambaldi, V., Malinowski, M., Tacchetti, A., Raposo, D., Santoro, A., Faulkner, R. et al. (2018), ‘Relational inductive biases, deep learning, and graph networks’, arXiv preprint arXiv:1806.01261 ., Monti et al. 2017Monti, F., Boscaini, D., Masci, J., Rodola, E., Svoboda, J. & Bronstein, M. M. (2017), Geometric deep learning on graphs and manifolds using mixture model cnns, in ‘Proceedings of the IEEE conference on computer vision and pattern recognition’, pp. 5115–5124.) are a type of neural network that takes graph structured data as an input. These are a very active area of reseach in Deep Learning due to their relational reseaoning and generalisation capabilities. There are many types of data we wish to learn that can naturelly be represented as graphs (e.g. social networks and molecular graphs). There are three major flavours of GNNs (Bronstein et al. 2021Bronstein, M.M., Bruna, J., Cohen, T. and Veličković, P., 2021. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478.) but we are only concerned with message-passing neural networks (Figure 5). A message-passing GNN is a model that takes a graph as input and calculates an output graph using the following:

\begin{equation} m_{ij} = \phi_\theta(h_i,h_j,e_{ij}) \end{equation} \begin{equation} AGG_i = \sum_{j\in\mathcal{N}(i)}^{}m_{ij} \end{equation} \begin{equation} h_i^{'} = \psi_\theta(AGG_i) \end{equation}

where h_i and h_j are the node features, e_ij are the edge features between two nodes and φ_θ is an MLP that constructs the messages m_ij. All the messages sent from the nodes in the neighbourhood of node i (N(i)) are aggregated together using some permutation invariant function (e.g. sum, mean or max). Finally, the node features at the next layer in the graph (h^'_i are calculated using ψ_θ which is an MLP. This is called the Update function. It is very common for GNNs to have multiple layers of message-passing steps and some sort of global pooling at the end if whole graph predictions are being made.