Section Contents
Discussion
A general observation is that the potentials learnt for simple distances and angles have minima in the right places but tend to be quite ”broad” in comparison to the force-field learnt in Greener & Jones (2021)
Greener, J. G. & Jones, D. T. (2021),
‘Differentiable molecular simulation can learn all the parameters in a coarse-grained force field for proteins’,
bioRxiv
doi:10.1101/2021.02.05.429941. This would mean that our model may allow too much conformational flexibility compared to the native dynamics of proteins, which will cause steric clashing and be a problem for many tasks (e.g. assessing the ’drugability’ of a binding pocket (Loving et al. 2014Loving, K.A., Lin, A. and Cheng, A.C., 2014. Structure-based druggability assessment of the mammalian structural proteome with inclusion of light protein flexibility. PLoS Comput Biol, 10(7), p.e1003741, doi.org/10.1371/journal.pcbi.1003741). However, it is notable that the slopes of all our learned potentials are much smoother, due to the fact we are using universal function approximators instead of refining individual bins, which is much more susceptible to noise.
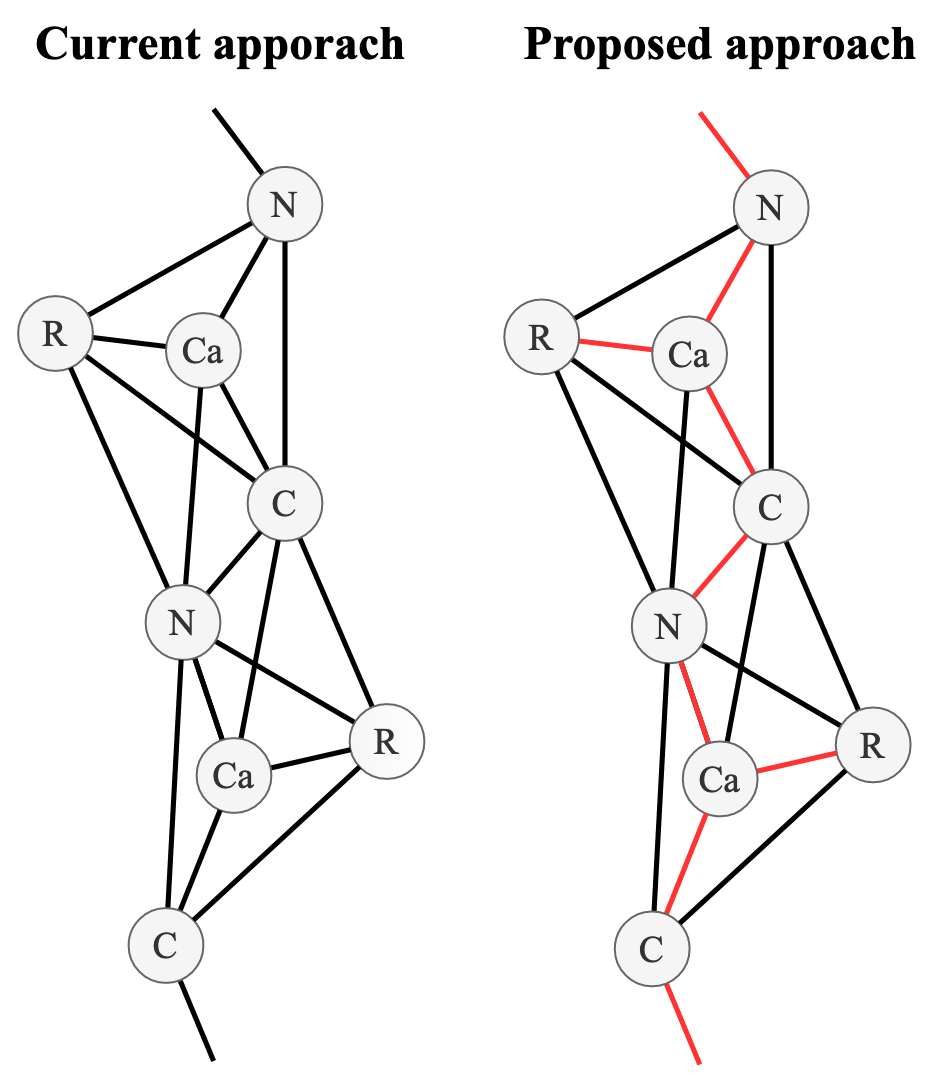
More importantly, the sidechain-sidechain interactions that stabilise the secondary and tertiary structure (Kathuria et al. 2015Kathuria, S.V., Chan, Y.H., Nobrega, R.P., Özen, A. and Matthews, C.R., 2016. Clusters of isoleucine, leucine, and valine side chains define cores of stability in high‐energy states of globular proteins: Sequence determinants of structure and stability. Protein Science, 25(3), pp.662-675, doi.org/10.1002/pro.2860.) were essentially unlearnt, even though MLPs should be able to approximate them in theory. This could be due to a number of factors; high learning rate, lack of exposure to tertiary flexibility due to insufficient number of time steps during training or a lack of signal-to-noise when compared to covalent interactions when minimising RMSD. We propose the latter issue could be resolved by creating 2 separate distance sub-networks, one for bonded and non-bonded interactions (Figure 10).
Our method also does not take into account any explicit solvent, which is problematic as protein folding and dynamics is largely facilitated by the hydrophobic effect (Bellissent-Funel et al. 2016Bellissent-Funel, M.-C., Hassanali, A., Havenith, M., Henchman, R., Pohl, P., Sterpone, F., Van Der Spoel, D., Xu, Y. & Garcia, A. E. (2016), ‘Water determines the structure and dynamics of proteins’, Chemical reviews 116(13), 7673–7697, dx.doi.org/10.1021%2Facs.chemrev.5b00664., Cheung et al. 2002Cheung, M. S., Garc ́ıa, A. E. & Onuchic, J. N. (2002), ‘Protein folding mediated by solvation: water expulsion and formation of the hydrophobic core occur after the structural collapse’, Proceedings of the National Academy of Sciences 99(2), 685–690, doi.org/10.1073/pnas.022387699.). This could be accounted for in the model by concatenating the solvent accessible area of every atom to its embeddings. Alternatively, simply concatenating the number of neighbours that every atom has would be a more efficient alternative.
In general, the RMSF analysis (Figure 9) showed that our method models considerably more flexibility in most parts of the two proteins we analysed. This is not surprising given the broad potentials seen in Figure 7. The BBA results would seem to suggest that the beta-strands tend to be modelled with more accurate flexibility than the alpha helical regions, with the second beta-sheet conforming to flexibility near that seen in the NMR ensemble. However, further analysis will need to be performed before any broad conclusions can be made. For example, the reduced RMSF seen in the second beta-sheet of BBA couple be due to the global alignment algorithms preference to align the structures along the beta-sheets as the alpha-helix detaches from the fold during simulation.
Given the quality of the learnt dynamics so far, considerable improvements will be needed before our approach can learn to fold small proteins, as was demonstrated with the learnt force-field in Greener & Jones (2021)
Greener, J. G. & Jones, D. T. (2021),
‘Differentiable molecular simulation can learn all the parameters in a coarse-grained force field for proteins’,
bioRxiv
doi:10.1101/2021.02.05.429941. Our dataset only contains small proteins (≤ 100 residues) too, meaning that the nature of inter-domain interactions will almost certainly not be learnt by any method trained on this dataset. However, the memory issues seen in our method, and protein DMS more generally, will need to be addressed before larger proteins can be considered for use in training. The KeOps library has also resulted in substantial memory improvements in other Geometric Deep Learning based approaches with proteins (Sverrisson et al. 2020Sverrisson, F., Feydy, J., Correia, B. & Bronstein, M. (2020), ‘Fast end-to-end learning on protein surfaces’, bioRxiv, doi.org/10.1101/2020.12.28.424589.) and future work could look into weather this could applied to other aspects of the DMS process (e.g. velocity integrators and energy calculations).
As was observed in Greener & Jones (2021)
Greener, J. G. & Jones, D. T. (2021),
‘Differentiable molecular simulation can learn all the parameters in a coarse-grained force field for proteins’,
bioRxiv
doi:10.1101/2021.02.05.429941, like deep learning, DMS is sensitive to hyperparameters. Our method has the additional complication of the neural network hyperparameters which also need to be refined to balance expressivity against memory requirements (as well as finding an optimum value of K) and is on going at the time of writing this report. Residual connections were added between the layers in the MLPs but this did not substantially increase performance.
By far the biggest limitation of our approach is the high memory costs incurred at each time step due to our use of neural networks to predict the potentials. For every atom interaction, angle and dihedral, a whole MLP worth of activations needs to be stored for AD, in stark contrast to Greener & Jones (2021)
Greener, J. G. & Jones, D. T. (2021),
‘Differentiable molecular simulation can learn all the parameters in a coarse-grained force field for proteins’,
bioRxiv
doi:10.1101/2021.02.05.429941 which only activates the values in two adjacent energy bins to calculate gradients. While it should be noted that we simulated our proteins over considerably fewer timesteps than in Greener & Jones (2021)
Greener, J. G. & Jones, D. T. (2021),
‘Differentiable molecular simulation can learn all the parameters in a coarse-grained force field for proteins’,
bioRxiv
doi:10.1101/2021.02.05.429941, so the comparison is only fair at short timescales, the results are still impressive given the substantially faster training time (~100x) and more efficient use of training data (1 epoch down from 45). This is a testament to the generalising and learning power of modern deep learning that suggests these methods are promising given more training time and hyperparameter refinement.
Future work
Equivariant Message Passing Networks
Recent work in the literature has addressed many problems with using GNNs on graphs where the nodes have spatial coordinates by endowing models with equivariance in the Euclidean group E(3) (Satorras, Hoogeboom & Welling 2021Satorras, V. G., Hoogeboom, E. & Welling, M. (2021), ‘E(n) equivariant graph neural networks’, arXiv preprint arXiv:2102.09844.). The E(3) group describes the sets of transformations that an object experiences in Euclidean space (translations, rotations and reflections). An example of translation invariance is provided in Figure 11. This is desirable for molecules as we would like these coordinates to be transformed in the same way that they would be transformed in real space. These methods have proved very effective in small molecule generation (Satorras, Hoogeboom, Fuchs, Posner & Welling 2021Satorras, V. G., Hoogeboom, E., Fuchs, F. B., Posner, I. & Welling, M. (2021), ‘E(n) equivariant normalizing flows for molecule generation in 3d’, arXiv preprint arXiv:2105.09016.) and it is speculated that AlphaFold2 relies on an iterative equivariant architecture (Fuchs et al. 2021Fuchs, F. B., Wagstaff, E., Dauparas, J. & Posner, I. (2021), ‘Iterative se (3)-transformers’, arXiv preprint arXiv:2102.13419.).
However, we argue that E(3) equivariance is not suitable for protein structures as it does not preserve the handedness (chirality) of their structures. Instead, we propose the use of the special Euclidean group SE(3) as these are equivariant to rotations and translations but not reflections. These architectures currently exist (Fuchs et al. 2020Fuchs, F. B., Worrall, D. E., Fischer, V. & Welling, M. (2020), ‘Se (3)-transformers: 3d roto-translation equivariant attention networks’, arXiv preprint arXiv:2006.10503 .) but are more computationally expensive than their E(3) counter-parts (Satorras, Hoogeboom & Welling 2021Satorras, V. G., Hoogeboom, E. & Welling, M. (2021), ‘E(n) equivariant graph neural networks’, arXiv preprint arXiv:2102.09844.).
Message Passing Simplicial networks
Another recent addition to the literature is Message Passing Simplicial Networks (Bodnar et al. 2021Bodnar, C., Frasca, F., Wang, Y. G., Otter, N., Montu ́far, G., Lio, P. & Bronstein, M. (2021), ‘Weisfeiler and lehman go topological: Message passing simplicial networks’, arXiv preprint arXiv:2103.03212.), which allows message passing on Simplicial Complexes (SCs). SCs are topological objects which generalise graphs to higher dimensions. This allows them to capture the higher-order interactions present in complex systems (e.g. molecules and biological networks). The authors also showed that MPSN had greater expressive power compared to baseline GNNs when learning regular graph and can be equipped with orientation equivariant layers. We propose that MPSN could be used to model the multi-level interactions (atom, residue, motif and domain level) we see within proteins. For example, if the potential between 2 atoms is known, and a third atom is introduced, it will distort the electron cloud of the other atoms, thus changing the potential (Goel et al. 2020Goel, H., Yu, W., Ustach, V. D., Aytenfisu, A. H., Sun, D. & MacKerell, A. D. (2020), ‘Impact of elec- tronic polarizability on protein-functional group interactions’, Physical Chemistry Chemical Physics 22(13), 6848–6860, doi.org/10.1039/D0CP00088D.). To the best of our knowledge, these effects have yet to be taken into account by any machine learning method to date.
Initial analysis into the feasibility of this approach indicated there were a prohibitive number of 2-simplices (triangles) in the course-grained protein graph at biologically relevant connectivity thresholds (∼ 8 Å). Further work could try to alleviate these issues by constructing a policy that only draws 2-simplices between 3 atoms types that are deemed biologically relevant (e.g. only between sidechain centroids within a certain distance or involved in a catalytic triad (Carter & Wells 1988Carter, P. & Wells, J. A. (1988), ‘Dissecting the catalytic triad of a serine protease’, Nature 332(6164), 564–568, doi.org/10.1038/332564a0.).