Symbolic distance matrices with KeOps
It is very common in structural bioinformaics to calculate distance matrices between all the atoms in a protein. These encode the 3D representation of the structure in a way that is invariant to the rotations and translations of the protein coordinates and are commonly used in protein structure prediction and molecular dynamics. However, the size of the distance matrix increases with the square of the sequence length, making this a significant limitation in DMS due to the requirements of AD.
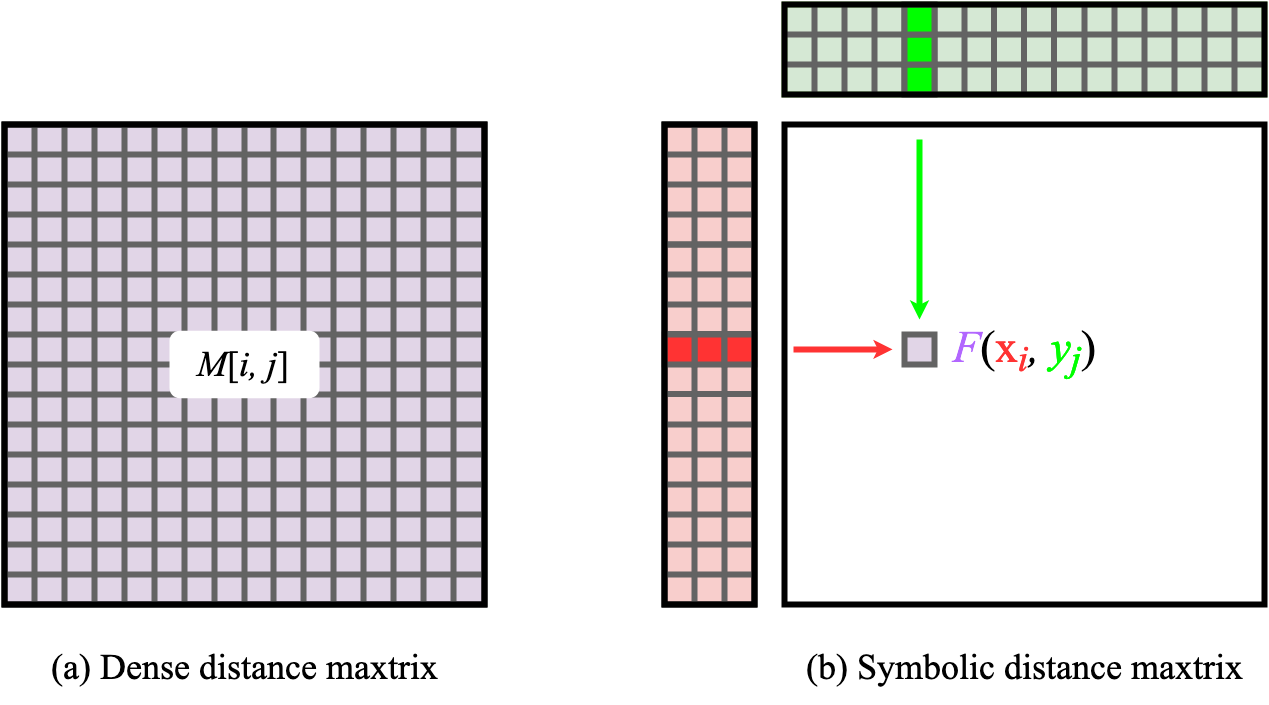
As this is a common issue in the field of Geometric Deep Learning, the KeOps (Feydy et al 2020Charlier, B., Feydy, J., Glaun`es, J., Collin, F.-D. & Durif, G. (2021), ‘Kernel operations on the gpu, with autodiff, without memory overflows’, Journal of Machine Learning Research 22(74), 1–6.) package has been developed to solve many of people problems. KeOps allows for reductions on large matrices (e.g. KNN calculations) that otherwise would not fit on the GPU memory. This is done through the use of symbolic distance matrices (Figure 6). Instead of storing a large matrix populated with precomuted values, symbolic matrices simply store the data required to generate the matrix (e.g. two vectors/matrices) and the equations needed to compute the elements in the matrix. In the case of protein distance matrices, the only data stored are the Cartesian coordinates of every atom (x and y, where x is the transpose of y) and the Pythagorean theorem to compute distances. This allows for substantial reductions in memory costs as the whole distance matrices is not stored in the main GPU memory and happens much more effectively using lower-level computations. In our case, we can effectively compute which are the K-nearest neighbours without needed to calculate a whole dense matrix in the GPU memory.